2022国考职位表什么时候发布?根据历年国家公务员考试职位表公布时间来看，2022国考职位表公布时间大概率在10月中下旬。请收藏此链接：2022国家公务员考试职位表下载-全国各省职位表，今年国考职位表一旦出来了，将会同步更新。以下为2021国家公务员职位表招录人数情况及近三年国考入面分数线，供各位考生参考了解：
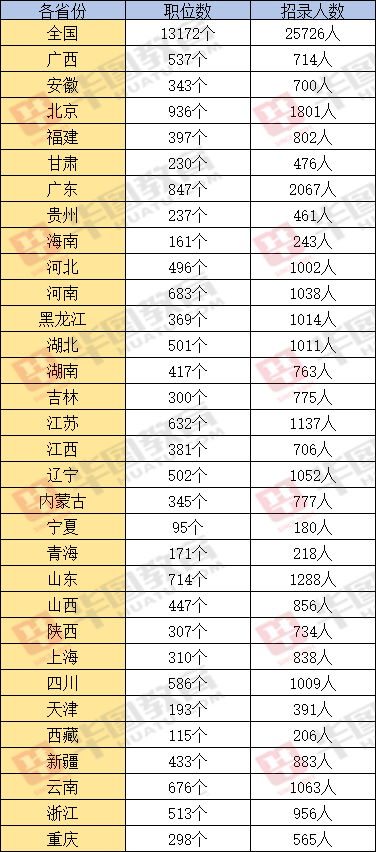
2021国考职位数量及招录人数情况表
2022年国家公务员考试很快就会发布公告，对于考生来说，历年的报考数据与入面分数线对自己设立备考目标有很大的参考价值，今天，华图教育就为各位考生准备了近三年国家公务员考试各系统报考人数以及分数线的相关资讯，供各位考生参考了解!
| 税务系统 | 年份 | 招录人数 | 职位数 | 平均竞争比 | 报名人数 | 分数线 |
| 2021 | 14942 | 7396 | 57:1 | 75万+ | 90.3-148.7 | |
| 2020 | 14894 | 8335 | 46:1 | 69万+ | 95.3-156.6 | |
| 2019 | 6046 | 4228 | 90.6:1 | 55万+ | 86.2-146 | |
| 统计局 | 年份 | 招录人数 | 职位数 | 平均竞争比 | 报名人数 | 分数线 |
| 2021 | 561 | 502 | 161:1 | 65506 | 90-141 | |
| 2020 | 643 | 558 | 88:1 | 56727 | 99.7-152.4 | |
| 2019 | 1330 | 1067 | 86:1 | 113996 | 85-137.6 | |
| 海关系统 | 年份 | 招录人数 | 职位数 | 平均竞争比 | 报名人数 | 分数线 |
| 2021 | 1538 | 668 | 40:1 | 61495 | 90-143 | |
| 2020 | 1530 | 731 | 54:1 | 88986 | 52.4-152.8 | |
| 2019 | 541 | 257 | 137:1 | 74199 | 89.9-140.7 | |
| 海事局 | 年份 | 招录人数 | 职位数 | 平均竞争比 | 报名人数 | 分数线 |
| 2021 | 945 | 646 | 59:1 | 56046 | 90-143 | |
| 2020 | 847 | 1264 | 84:1 | 71585 | 96.3-153.8 | |
| 2019 | 1168 | 827 | 47:1 | 55324 | 85.1-141.7 | |
| 铁路公安 | 年份 | 招录人数 | 职位数 | 平均竞争比 | 报名人数 | 分数线 |
| 2021 | 1021 | 449 | 10:1 | 1.3万+ | 46.09-67.17 | |
| 2020 | 1134 | 483 | 29:1 | 32410 | 49.69-69.77 | |
| 2019 | 1232 | 602 | 91.5:1 | 112847 | 87.18-135 | |
| 银保监会 | 年份 | 招录人数 | 职位数 | 平均竞争比 | 报名人数 | 分数线 |
| 2021 | 710 | 523 | 64:1 | 45627 | 45.17-71.87 | |
| 2020 | 1030 | 641 | 57:1 | 66234 | 47.8-74.7 | |
| 2019 | 1214 | 784 | 73:1 | 88355 | 90.75-152.5 | |
| 出入境边防检查总站 | 年份 | 招录人数 | 职位数 | 平均竞争比 | 报名人数 | 分数线 |
| 2021 | 649 | 293 | 57:1 | 4.2万+ | 45.56-68.67 | |
| 2020 | 575 | 194 | 35:1 | 2.3万+ | 51.69-68.27 | |
| 2019 | 136 | 32 | 45:1 | 0.6万+ | 48.9-64.1 | |
以上就是华图教育专家对 2021年国考职位表进行的深度解读，希望22考生可以在知己知彼的基础上好好复习，争取一战上岸!
为帮助各位小伙伴可以更早、更好为2022国家公务员笔试做准备，图图在这里特地为大家带来了国家公务员笔试行测资料，希望对各位小伙伴的笔试备考起到帮助。
国考笔试课程>>>2022国家公务员考试红领决胜全程营
国考笔试课程>>>2022年国家公务员笔试系统提升班
国考备考图书>>>2022国考基础6本套：教材+真题+同步练习册
国考备考图书>>>2021国家公务员考试申论33套+行测3600题库3本装
行程问题在大多数同学的脑海里就是一团乱麻，剪不断，理还乱，尤其是多次相遇追及问题，相遇个两次三次还能勉强理清楚，但是相遇次数过多，那就基本是OVER!其实大多数多次相遇追及问题并不是那么可拍，而是“纸老虎”，只需要一个公式就能一步到位得出答案。今天我们就来揭开这层纸，看看这只“老虎”有多凶?
多次相遇问题在考试中出现的频率比较高，我们着重来讨论一下多次相遇问题。多次相遇一类问题中大家比较熟知的应该是从两端出发的多次相遇问题，其实历年考题中还考过另外一种单端出发多次相遇问题，下面我们分别进行分析：
两端出发多次相遇：我们可以借助一个场景先来帮助大家理解，在道路两端A、B，分别有甲、乙两人同时出发。甲从A点出发前往B点，乙从B点出发前往A点，他们到达对方的位置之后并没有停下来，而是再继续返回，在两者共同运动的过程中，两人会出现相遇很多次的情形，这就是两端出发多次相遇问题。接下来我们借助图形来推导一下相关公式：
由图可见，除了第一次相遇之外，后续每相遇一次，就会多一个2S，如果相遇N次，共同走的距离S=S+(N-1)2S=(2N-1)S，即两端出发多次相遇的公式为：(2N-1)S=(V1+V2)T。
单端出发多次相遇：同样借助一个场景来理解一下，甲乙两人都在A段，其中甲速度较大，两人同时出发，甲先到达B端，再反过来回到A端，就能与乙相遇。同样都是两个人在AB两端不停的运动，整个过程中，会出现两者多次相遇的情形。如图所示：
同样由图可见，每相遇一次就走一个2S，N次相遇就走2NS，故相遇N次，公式应该是：2NS=(V1+V2)T。
对公式相信同学们应该都有了一定的了解，接下来我们一起来看看真题。
【例1】在一次航海模型展示活动中，甲乙两款模型在长100米的水池两边同时开始相向匀速航行，甲款模型航行100米需要72秒，乙款模型航行100米需要60秒，若调头转身时间忽略不计，在12分钟内甲乙两款模型相遇的次数是?
A. 9
B. 10
C. 11
D. 12
【答案】C
【解析】本题问到相遇多少次，明显考的是两端出发多次相遇问题。根据两端出发多次相遇的公式：(2N-1)S=(V1+V2)T，代入可得：
，解得N=11.5，计算结果不是整数，此时的含义是，已经完成了11次相遇两人正在相遇第12次的路上。故选择C选项。
【例2】甲、乙两人同时从A、B两地出发，相向而行，甲到达B地后，立即往回走，回到A地后，又立即向B地走去;乙到达A地后，立即往回走，回到B地后又立即向A地走去。如此往复，行走的速度不变，若两人第二次迎面相遇的地点距A地500米，第四次迎面相遇地点距B地700米，则A、B两地的距离是：
A. 1350
B. 1460
C. 1120
D. 1300
【答案】C
从以上两道题可以看出，其实多次相遇的行程问题并没有想象中那么复杂，记牢公式，多练习，就可以快速解题，拿到高分，拾起我们最后一根救命稻草，上岸成公!
